I was most fascinated by “Sixteen Lilypads: An After Action Report” by Terry Trowbridge and Joseph Alexander Brown in Rampike 21/2. I tried to locate the original poem unsuccessfully on the net as I don’t have the bpNichol collection containing it. I could find the poem worked upon as a graph by the Trowbridge and Brown in their “Finding the Punchline” paper as below, and assume that the original poem is a 4×4 matrix with 16 variations of the letters in the word ‘frog’. The proposal below is based on this assumption.
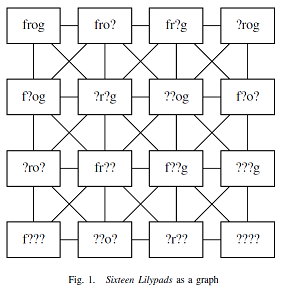
(Fig 1 presents the original poem completed with lines)
Part I
HEX: The hexadecimal number system in the poem
At the heart of this poem, is the reference to hexadecimal number system used in computer science and digital electronics. The hexadecimal number system is a system of counting in steps of 16 as opposed to the decimal system, which does in 10. The representation of numerals in this method is done by the elements, 0,1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F. Notice how the numbers extend from the decimal system’s set of (0-9) to English language alphabets (A-F). A to F are numerals in this system, and not alphabets in English any more. Conversely, the hexadecimal number language uses alphabets (0-9, A-F). This is the key to “Sixteen Lilypads”.
FROG: The word FROG as a leap beyond the hexadecimal language
The language of bpNichol leaps from the letter ‘F’. He uses the last letter of the chosen language of hexadecimal as the opening letter of the only word in the poem to present in a language familiar to others as English, but strange to himself. This helps him move further from ‘F’, and question (?) where these languages merge. The animal he wants for his poem should start with the letter ‘F’.
Let’s look at the word construction: It’s made of English language letters, F, R, O and G. The earliest among these in alphabetic occurrence is ‘F’; all other letters are beyond them. bp is pushing language from ‘F’ further. A guess: he could have chosen an insect like FLEA to write the same poem, but that wouldn’t fit; he couldn’t have taken this leap in language with a FLEA. It contains the letters A and E making it fall back into the hexadecimal language and thus defy his purpose. bp would slip into the known realms of language.
A flea cannot fly away from the hexadecimal language; a frog leaps from it. The word ‘pads’ in the title suggests it.
The nature of movement of a frog is digital- it covers n yards in one go. This is the basis of digitization:
1 LEAP = N YARDS.
Notice the amphibian nature of the animal. FROG may slip into the surrounding water, but never die. At worst, it may land on the wrong lilypad: information may partially be destroyed, but never lost in the digital world.
?: bpNichol’s question mark’s functions and the Hamiltonian pattern
bpnichol’s way of making the strange familiar and the familiar strange is through this question mark. This has a critical and tricky function in the poem.
The mind of the lay reader substitutes the punctuation mark with variations of letters in the word FROG. It understands the mark as intriguing permutations and combinations. Trowbridge and Brown go one step further and join the dots lying around ‘FROG’ to discover a ‘Hamiltonian’ pattern.
The proverbial animal known to constrain itself within its surroundings suddenly appears to behave hamiltonianly. So far Trowbridge and Brown succeed in identifying strangeness in a most familiar creature. bpNichol’s frog is Hamiltonian. The adjective is strange to the non-scientific reader, and bpNichol is thus seen to observe even the most familiar animal in an unfamiliar way, ‘hamiltonian’ perhaps a strange adjective even to himself.
True and Complement Forms: Questioning the assumption of a Hamiltonian path
The error I see in the analyses by Trowbridge and Brown is the substitution of ‘?’ with the corresponding letters from FROG. bpNichol has masked the complement form of the Boolean variables, F, R, O and G by the punctuation mark. If the hexadecimal language extended into English language alphabets, then what were those alphabets that were the complement forms of F, R, O and G? What is F’? What is R’? What is O’? What is G’? They are not English; they are not commonplace numbers. In which domain do they exist?
‘Hamiltonian path’ may be an alien creature to the common man, but a frog in computer science. While the poem may be approached for its alphabets ‘F’ ‘R’ ‘O’ and ‘G’ through known algorithms, it should not be done so for ‘?’. Does an alien algorithm, A exist to connect the question marks? If A is figured out, then does a more alien algorithm than A exist? This is the spirit of bpNichol’s inquisitiveness hidden by ‘?’. As per the findings of Trowbridge and Brown, ‘?’ don’t connect as Hamiltonian graphs. I’m not sure if they can be classified under the category non-Hamiltonian.
Definition:
Non-Hamiltonian Graphs: Non-Hamiltonian graphs are those graphs that are not Hamiltonian
Then why is the Non-Hamiltonian graph still credited to Hamilton? ‘?’s in Sixteen Lilypads connect by a graph called ‘?-graph’ or bp-graph. It’s Nicholian.
Karnaugh Maps: The possibility of a whole new map of logic variables
Karnaugh maps or K-maps are frequently used in digital circuit design for logic simplification.
To give an example, here’s a K-map with 2 variables, A and B:
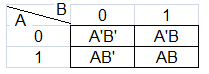
The map contains exact number of squares as 2n for n-variables. Thus a 2 variable K-map contains 4 boxes, each taking the logic value of one possible combination of the variables A and B in true and complement forms. The “truth table” of A & B is represented as a K-map.
E.g., If A is true and B is true, then the entry for the combination, AB takes the Boolean value 1.
This can be extended to a 4 variable K-map shown below:

A K-map representation of logic equation can be used for a small set of variables. It is compact and easy to use for a maximum of 4 variables. In rare cases, 5 variable K-maps are used. K-maps are not used beyond that as they become unwieldy.
bpNichol’s “FROG” resembles such a logic map, but not exactly a K-map. It employs a frequent matrix of the map (4×4) but differs in the aspect that in a K-map, adjacent entries change only one variable at a time.
bpNichol was reinventing a map for logic variables. I call it a “?-map”, and don’t plan to analyze here whether it is one of the predecessors of K-map or a successor. His intention was not to solve a logic equation, but to question language itself. In doing so, perhaps he either made a cliché or a scientific invention: If he reinvented maps that were not optimal, and that couldn’t be “used”, he was 100 years backward; he didn’t pay enough attention to his peers and pioneers in the other field. If by intuition, he arrived at a combination that has not yet been discovered by engineers and computer scientists as “useful”, he was 100 years ahead of his time.
Butterfly Effect?
The alphabets F’, R’, O’ and G’ complement F, R, O and G. They exist as duals, but the complementary forms are mysterious. How do F, R, O and G echo? Moreover, if the frog falls into the pond of information, what are its repercussions? The poem is a play of light and dark. Does something akin to Butterfly Effect exist in the behavior of frogs? What is unknown about it? Do these observations by bpNichol reveal him as a biologist?
The ?-map can be swapped along some of its rows and columns to resemble a K-map. The entries of a K-map then seem to connect by a “Hamiltonian Graph”. Was Karnaugh aware of such a connection when he created his maps? Does it make him more graphically sound than he was?
Part II
?-Poetry: The connection between mathematics and poetry
The act of finding a Hamiltonian path by connecting elements by straight lines is not distinct from the act of writing poetry. Random examples are poems by Michael Winkler (Which of his texts are Hamiltonian, and which, non-Hamiltonian?), and Richard Parker (A poem is modulation/demodulation. It is an act of retrieving signal from noise; a good poem has an SNR of 89.75dB.) in the same issue of Rampike.
The graph in Fig.1 as worked upon by Trowbridge and Brown is thus a poem, unintentionally. But this finding won’t add to the effective poetic capability, P in Hamilton, unlike how the Trowbridge and Brown findings set out to add a ∆ to bpNichol’s overall Mathematical Knowledge. M. bpNichol was mathematically talented, the findings enhance it. Expressed differently, bpNichol had a mathematical dumbness of ∆ so far, the proposal seems to remove it.
Basho: Conceptual translation of Matsuo Basho’s haiku and the Atomic Structure
bpNichol uses lilypads as his springboards.
Within the skylark’s song –
the distinct rhythm of
the pheasant’s cry.
A Translation:
A warbler singing –
somewhere beyond the willow,
before the thicket
A Translation:
A translation of haiku by Basho as these may reveal cosmic arrangement, atomic structure or one in the other.
[Source of English text for Basho’s haiku above: Narrow Road to the Interior, Matsuo Basho translated by Sam Hamill; conceptual translation, mine]
Thiruvaimozhi: A further example on visual and mathematical representation of a literary work
I’d like to present an aspect in the structure of Thiruvaimozhi, a work of Tamil antiquity by Nammalvar, also known as Kurugur Satakopan, transmitted by word of mouth to his disciple, Madhurakavi, and compiled much later, in the 9th-10th century AD by Sri Nathamuni. The poem is translated by Srirama Bharati as “The Revelation: A Morality Play of Kurugur Satakopan”.
Thiruvaimozhi is a continuous chain of 1000 poems knit together as a single long work. The poem is divided into 100 sets. The poet adds a signature 11th poem to each set of 10 poems making reference to the work on hand as “these 10 of the thousand by Kurugur Satakopan”. The poet thus creates an oddity in composition while he could have stuck to the perfection of 10 and 1000; he need not have written in misnomers.
This addition of a single poem per 10 seems to self-correct and move towards the expectation of roundness in quantity because these errors add up to a perfect 100 at the end of 1000 poems. But Nammalvar mysteriously adds 2 poems to one of these sets of 100 so that the particular set contains 13 poems including the signature poem. Totally, Tiruvaimozhi contains 1102 poems though they are referred to as 1000.
The structure of a decad of these poems can be represented as:
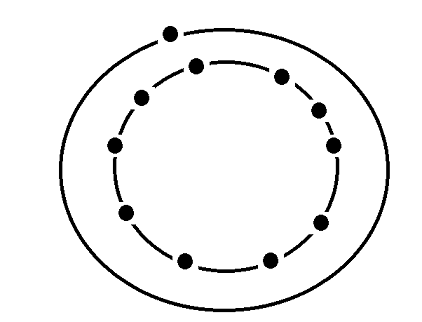
It makes the poem volatile. If the orbit of the poem were complete with a round number, the poem would not react, like an inert element. The disturbance by a single signature poem gives the structure a valency of 1 in this case.
If a hypothetical atomic structure were allowed to take 10 electrons in its first shell, and 100 in the 2nd, the 100 sets of 10 poems each would form a molecule. The excess two poems still exist in an orbit further outside preparing the composition for polymerization.
The poet writes into himself, and opens up for others of his kind to write in. Tiruvaimozhi, along with poems by 11 other poets, forms a part of the text of “4000 poems”.
Form reveals content.
It is impossible to associate knowledge of atomic sciences and chemistry to Nammalvar as the poems are dated much before Dalton’s and Bohr’s discoveries.
Conclusion: A few words for idleness and cowboys
Life is difficult. It appears from the Trowbridge & Brown’s call for collaboration, that today’s research scientists, activists and poets refresh us with such poetry, criticism and interdisciplinary studies in their spare time; poets like bpNichol had time enough to fart and write.
The essay displays an individual intelligence, ‘I’ and calls for a collective intelligence, ‘V’ to ascertain bpNichol’s mathematical brilliance. I believe bp derived from existing forms in the universe. If we accept the proposed increase in the variable M (referred to in an earlier section), then we shouldn’t be surprised if an association of cowboys comes up with a paper, “Was bpNichol a cowboy and not a poet?”
