Introduction: The grammar machine
”Building a circuit is like building a sentence”, says American journalist and author T.R. Reid in his book, “The Chip: How Two Americans Invented the Microchip and Launched a Revolution” published in 1985. He adds, “There are certain standard components— nouns, verbs, adjectives in a sentence; resistors, capacitors, diodes, and transistors in a circuit— each with its own function.”
The grammarian, Paul Roberts introduces English grammar in his book, “English Sentences” published in 1962 thus: “… Grammar is something that produces the sentences of a language. An English grammar would be a set of rules for making English sentences. Or we might think of that “something” as a machine with rules built into it. It is possible to conceive— it might even be possible to build— an electronic machine that, by following its rules, would come out with an English sentence every time it went through its operation and that never would produce a non-English sentence.”
Two practitioners of different fields, say of linguistics and electronics think like each other, and complement each other, one borrowing from the other’s domain. I thought of a hypothesis then: what if circuits are fed with words instead of electrical signals? Would that reveal circuits in a dimension hitherto unknown to us?
Rohmeo and his transistors

I took up a job with ROHM Semiconductor, a Japanese chip making firm in 2015.
The name of the company is a wordplay in itself. Establishing the company in 1958,
Ken Sato-san transmitted a proper noun from the circuit language into the world. The resistor is normally represented in short by “R” in a circuit, and its value is measured in Ohms; “R” and its unit “Ohm” are usually seen together in a circuit diagram; the quotidian observation of a component maker converted itself into a proper noun. Our internal magazine is called “ROHMANTICA”, and I wondered if men at workplace fancied themselves as ROHMeos, what would the women consider themselves as!
Nevertheless, the world of Integrated Circuits is populated with transistors, and they are of two types: P and N. Sometimes designers call a special function transistor, if it is a P-type, Fred, and if N-type, Judy.
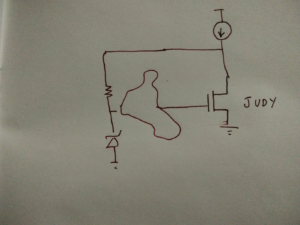
The output transistor of a Low Dropout Regulator is sometimes called MOAG (The Mother of All Gates) or simply, the ‘Mother’ transistor. So natural language is already present in the way engineers have named the components in the world of circuits. Thus, circuits themselves can be seen through the lens of natural language including intended and unintended meanings it holds.
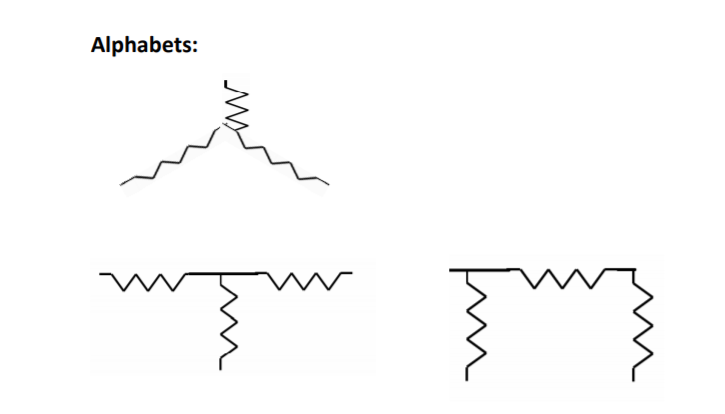
And, when they resemble the alphabets of a language, like Π and Δ of Greek, or, T or H of English, they are named so.
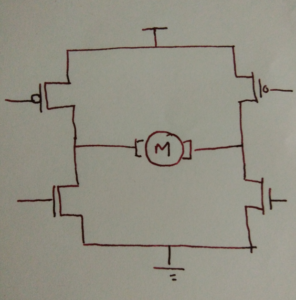
However, a fallacy exists in the arguments so far: the human mind associates itself with the circuits and gives it a human language so the circuits seem to have a human language. The conclusion seems right because an assumption is made at the outset about the conclusion. What if a cat looks at the H-bridge? Will it appear as “H” to it even if circuits are of no consequence to cats?
“I like the little they know,
which is so
much.”
(from “my cats” by Charles Bukowski)
The Accents of French and the Direction of Electric Current
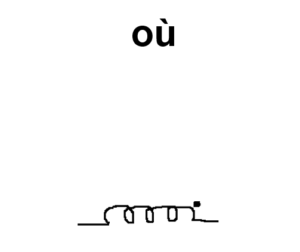
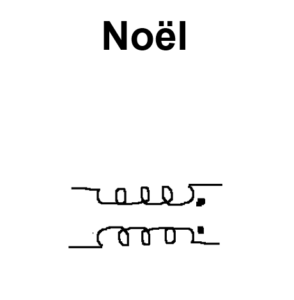
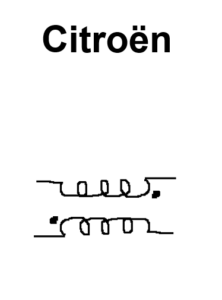
From ‘Talking Circuits’, Chapbook by SS Prasad published by Offerta Speciale, Italy, 2014.
Just as an accent shall alter the pronunciation of a given alphabet, the DOT convention indicates the direction of entry of current and the polarity of mutual inductance. Note that the assumption at the outset in the circuit is devoid of human language.
Applying the Tenets of a Classical Language to Circuits: Employing Sanskrit
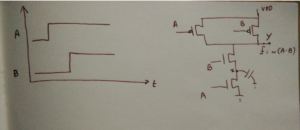
Consider a simple NAND gate shown in the figure that gives an output of 0 only if both the inputs, A and B are 1; otherwise, its output is 1. Though the function is commutative, i.e., ~ (A.B) = ~ (B.A) logically, which combination would be optimal for, let us say, speed?
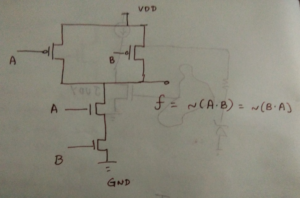
If we know that the signal A always appears earlier than the signal B, then the signal A is placed on the NMOS closer to GND. Thus, the node x is evaluated in the duration the gate tied to B waits for its input.
Dwandwa Samas
Word combination and word order of a compound word are defined by ‘SAMAS’ in Sanskrit. Dwandwa Samas is one particular rule for word order.
Example: RAMA + KRISHNA = RAMAKRISHNA
The rule lays it out that the words are arranged in increasing order of syllables. However, exemptions can be made depending on the importance of certain words.
Example: SMRITI + ITIHASA + PURANA = SMRITI-ITIHASA-PURANA ITHIHASA, though 4 syllables, precedes the 3-syllabled PURANA because of the importance given to it in literature.
The logic gate input priority selection can be viewed as a ‘Dwandwa samas’ application in circuit.
Katapayadhi Sankhyay
Katapayadhi sankhyay is a scheme of associating weights with alphabets: each alphabet in the alphabet chart is given a weight in Sanskrit. In some applications, the weights are used in encoding as in Carnatic music: the 72 chief ragas are named such that the position of the melody in the list can be decoded from the first two alphabets of their names.
In Vishnu Sahasranamam, the oral poem by Bheeshma in which he extols the qualities of Vishnu in his thousand names in the ”Mahabharata”, the word RAM is used thrice in succession to indicate a thousand.

Katapayadhi sankhyay could be thought of as associative with amplification.
The Vision of a Crow: The Kaakakshi Maxim
A crow can see only with one eye. Really? Perhaps an exaggeration. A crow can see only one angle at a time.
The maxim is applied in elaborating the meaning of certain mantras. One word in the mantra looks at all other words in it, one word at a time thus revealing its meaning.
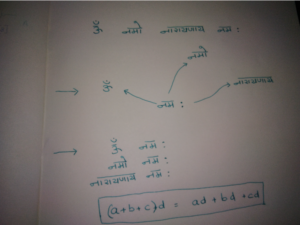
The aforementioned maxim could be applied to any n words. The MOSFET with its 3 terminals used in amplifiers is often looked “into” its terminals for their impedances.
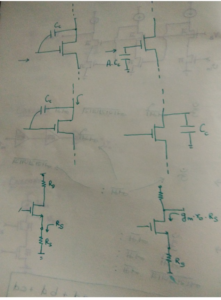
Conclusion and a beginning
I have so far analysed circuits randomly, though not systematically and proposed that circuits could be viewed and analysed on the same terms as languages. Perhaps Kirchoff’s Law, Ohm’s Law and the several other laws in the circuits as identified by the accredited scientists and engineers are only pre-existing grammatical laws of a time-tested language.
It is also possible to show how language could be viewed as circuits.
Across
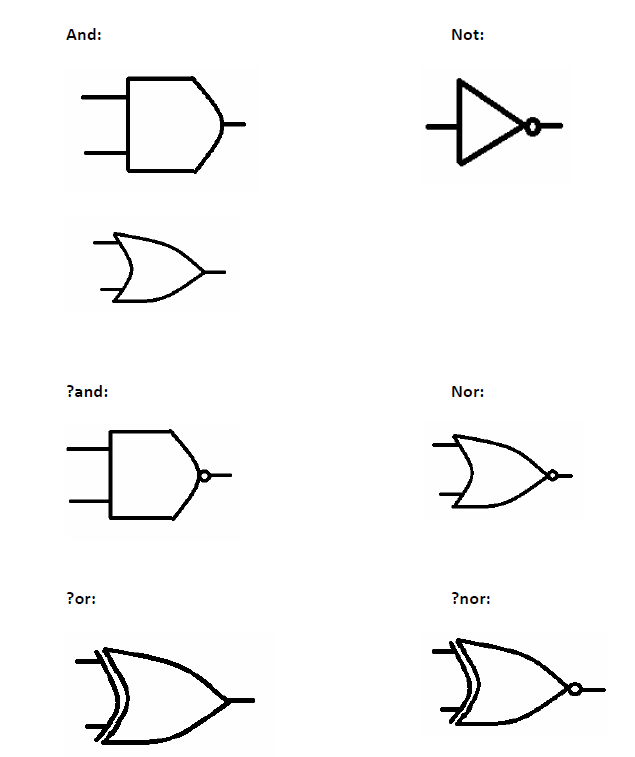
Logic as Conjunctions
The EX-OR has no correspondence in English.
EX-OR = ?-OR
Talking Circuits (Poems)
Telescope
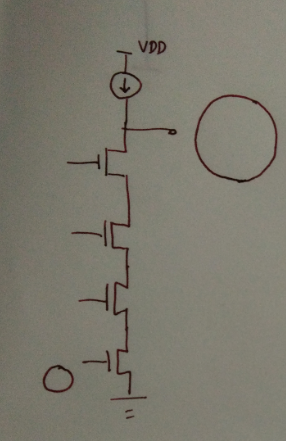
Tail
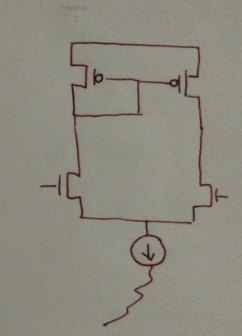
Kite
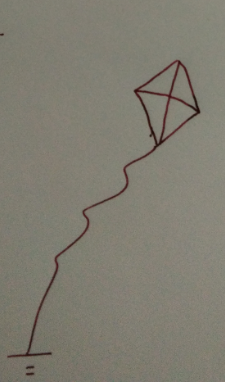
Lamppost

Wireless

